
SHA-256 或安全散列算法 256 位是一种加密散列算法/函数,目前几乎所有计算机都在广泛使用。
它属于 SHA-2 哈希算法系列,由美国国家安全局(NSA)开发,于 2001 年首次发布。
目前,这种算法的一些常用案例包括:
- SSL/ TLS 数字证书
- 比特币和其他加密货币的挖矿算法
- 生成比特币钱包地址
- 检查 Git 等版本控制系统中文件的完整性
- 密码散列、存储和验证
这篇博文深入探讨了这一算法,并手把手地教大家如何实现这一算法。
SHA-256的疯狂之处是什么?
散列函数/算法的基本工作原理如下
对于任何数据,散列函数都能生成其唯一的表示形式
SHA-256 是 Python 内置库 hashlib 中的一种方法,使用方法如下。
import hashlib
# Specify the input
input = "ashish"
# Convert it into bytes
input_bytes = input.encode("utf-8")
# Create a SHA256 Hash Object
hash_object = hashlib.sha256()
# Update the object with the byte representation
hash_object.update(input_bytes)
# Generate the hexadecimal representation of the hash
hash_hex = hash_object.hexdigest()
print(hash_hex)
# 05d08de271d2773a504b3a30f98df26cccda55689a8dc3514f55d3f247553d2b
SHA-256 散列函数之所以如此神奇,原因如下。
1、确定性固定输出长度
对于任意长度的数据,它都能返回一个唯一且精确的 256 位表示,每次计算都是一样的。
2、雪崩效应
如果输入数据发生变化,哪怕是很小的变化(一个比特),输出也会发生巨大变化(就像雪崩一样)。
#SHA256 representation of "ashish"
05d08de271d2773a504b3a30f98df26cccda55689a8dc3514f55d3f247553d2b
#SHA256 representation of "Ashish"
ff81423fd44fc0fb20422ffb699ce225bacb400fb70ee3fee3743aac45e910b4
3、抗碰撞
当两个不同的数据项产生相同的哈希值输出时,就会发生哈希碰撞。
以前的许多哈希函数都发现过碰撞,如 SHA1(碰撞由 Google 发现),但迄今为止,SHA-256 还没有发现过碰撞。
4、Pre-Image Resistance
图像 "是指应用哈希函数后的输出结果。
因此,‘Pre-Image Resistance’ 一词是指 "前图像 "或散列函数的输入无法通过输出("Image")计算出来。
这是因为每一个输入都有 2²⁵⁶ 个可能的输出哈希值,如果用目前的前量子计算技术尝试蛮力方法(即对每一个可能的组合进行试错),实现这一目标所需的时间将超过宇宙本身的年龄。
5、极快
SHA-256 算法速度极快。
在 Python 中使用 timeit 对其进行基准测试,结果显示其计算哈希值的时间仅为 1.2 微秒。
import hashlib
import timeit
def hash_a_string():
text = "ashish"
text_bytes = text.encode('utf-8')
hash_object = hashlib.sha256()
hash_object.update(text_bytes)
return hash_object.hexdigest()
number_of_runs = 1000000
# Using timeit to measure the execution time (Running the function 1 million times)
time_taken = timeit.timeit(hash_a_string, number=number_of_runs)
average_time_per_run = time_taken / number_of_runs
average_time_per_run_microseconds = average_time_per_run * 1e6
print(f"Average time per run: {average_time_per_run_microseconds:.3f} microseconds")
# Average time per run: 1.244 microseconds
我一直很好奇,为什么神经网络无法逆转 SHA-256 哈希值。
通过学习它的复杂性和手工计算,我找到了答案。
所以,如果你也有同样的遭遇,读完这个故事你也会得到答案。
现在是深入研究其实施的时候了。
用密码学 "玷污 "我们的双手
我们的任务是计算字符串 ashish 的 SHA-256 哈希值。
步骤 1:将字符串字符从 ASCII 转换为二进制
首先使用下表将字符串的 ASCII 字符转换为二进制。
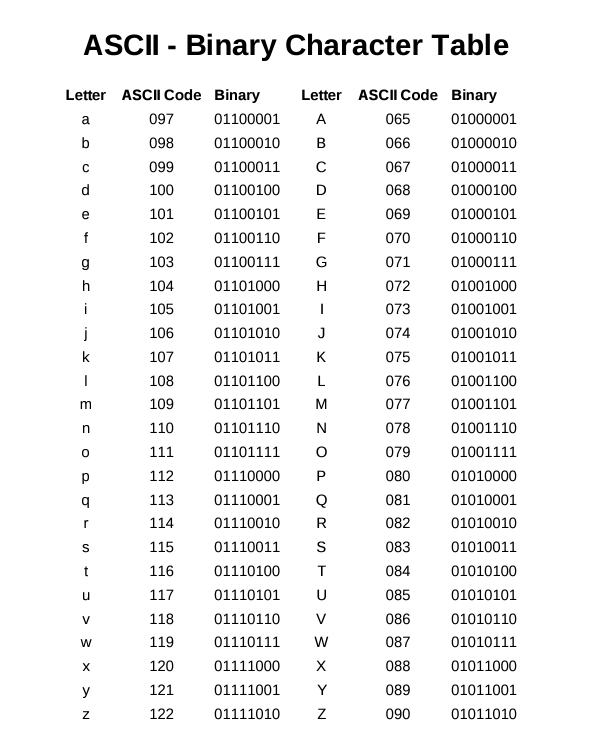

这些二进制表示法的连接方式如下

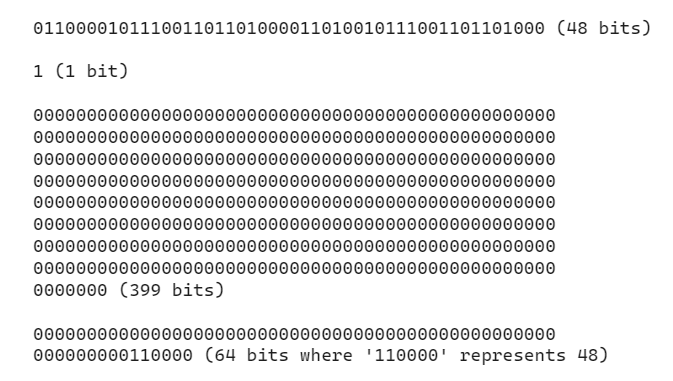
步骤 2:填充信息
这一步的目的是使我们的输入是 512 位的倍数。
为此,在上述比特的末尾加上比特 1,然后再加上 0,使长度为 448mod512。
因此,448 - (1 + 48) 或 399 个零被加入其中。
为什么是 448mod512?- 你可能会问
这就确保了我们的数据块在经过原始输入和填充后,长度字段的剩余位数正好是 64 位。
接下来,输入长度(二进制)会被加进去。
在我们的例子中,这是 48 位,即二进制的 110000。
步骤 3:将填充输入分割成 N-512 比特块
由于我们的输入只有 512 位,在我们的情况下,N = 1。
换句话说,我们只有一个 512 位的单一数据块需要进一步处理。
步骤 4:将填充后的输入分割成 32 位字
512 位输入被分成以下 16 个 32 位字,每个字都标有 M(0)至 M(15)。

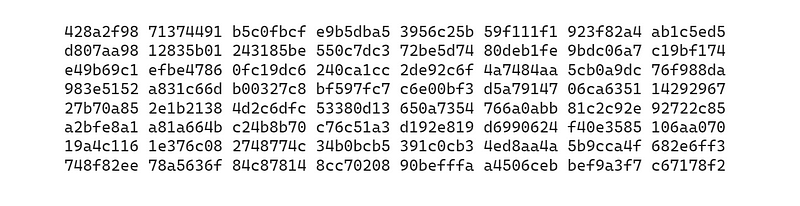
步骤 5:设置常量
这一步涉及在我们的算法中使用质数的特性。
在这一步中,我们取前 64 个质数,计算每个数的立方根。
然后,获取立方根分数表示(二进制)的前 32 位,并转换为十六进制。
这些值表示为 K(n),其中 n 的范围为 0 至 63。
这些数值从左到右从 K(0)到 K(63)如下所示。
步骤 6:设置初始哈希值
在这里,我们要做的与上述步骤类似。
我们通过取前八个质数平方根的分数部分(二进制)的前 32 位,计算出八个值,用 H(0)(n)表示(我们将进一步研究)。
例如,对于第一个质数 2,它的平方根 √2 ≈ 1.4142135623730950488016887242097。
我们保留其小数部分,并将其转换为二进制,即 01101010000010011110011001100111,然后转换为十六进制,即 6a09e667。
这就是我们的 H(0)(0) 值。
我们对所有前 8 个质数都这样做。

SHA-256 哈希计算
我们对填充输入的每个 512 字段(本例中 N= 1)进行处理,并采取以下步骤
步骤 7:准备信息时间表
我们计算出六十四个 32 位值,用 W(t) 表示,其中前 16 个值(W(0) 到 W(15))正好等于步骤 4 计算出的 M(0) 到 M(15)。
W(t) 的其他值(从 W(16) 到 W(63))按以下公式计算-- W(16)
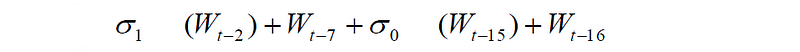
在上述公式中,σ(0)和σ(1)由以下等式给出-- σ(0)
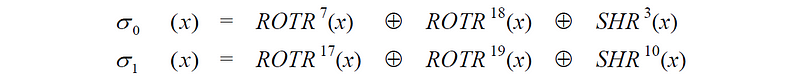
ROTR和SHR等术语可能看起来隐晦难懂,超级令人困惑,但让我们了解一下它们,不要失去希望。
ROTR(n)(x) 表示对输入 x 的 n 位进行右旋。
例如,ROTR(1)(011) 表示 011 中 1 位的右旋。
操作结果为 110。
最后 "脱落 "的那一点被添加到左边,因此被称为旋转。
SHR(n)(x) 表示输入 x 中 n 个比特的右移。
例如,SHR(1)(011) 表示在 011 中右移 1 位。
操作结果为 001。
在这个操作中,"脱落 "的最后一位不会被旋转,而是从左边加上一个 0。
现在你知道这些是什么了,σ(0) 和 σ(1) 只是对其组成值进行 XOR(排他 OR)运算 (⊕) 的结果。
利用这些值,对 W(16) 到 W(63) 的值进行 2³² 模加法运算(公式中的 + 号表示运算),即可计算出 W(16) 到 W(63) 的值。
这一操作的结果是这些 W(t)值的 32 位结果。
Example: Calculation Of W(16)
这里可能会出现一些混乱,让我们以计算 W(16) 为例进行说明。
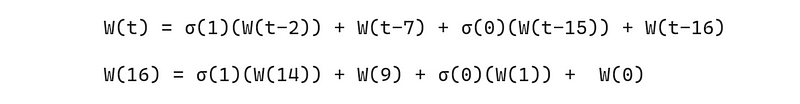
让我们转到 σ(1)(W(14)),它与σ(1)(M(14))相同。
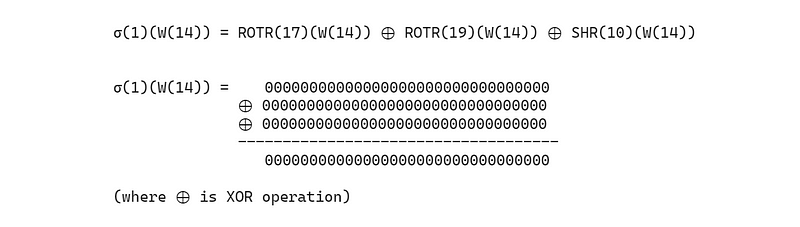
同样,σ(0)(W(1)) 与 σ(0)(M(1))相同,计算公式如下。
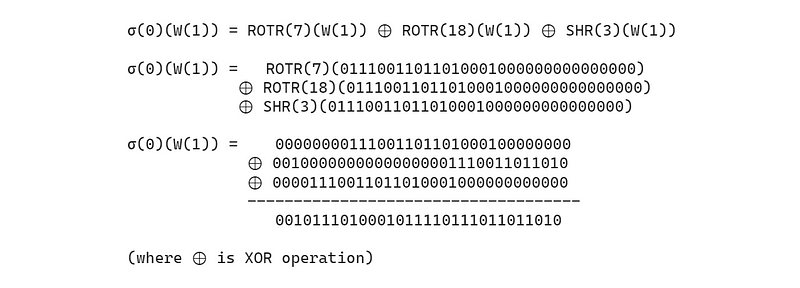
最后,让我们执行最后一步。
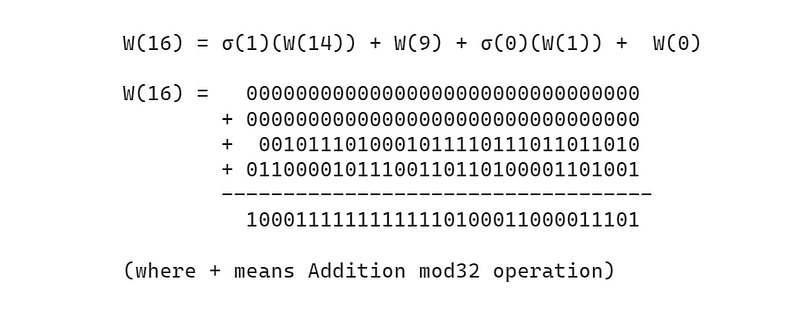
从 W(17)到 W(63)的进一步计算也同样进行。
步骤 8:用初始 H 值初始化八个变量
8 个变量(从 a 到 h)使用之前计算出的 H 值进行初始化,如下所示。

步骤 9:对这些变量执行进一步操作
接下来,在 t = 0 到 t = 63 的循环中对上述变量执行以下操作。
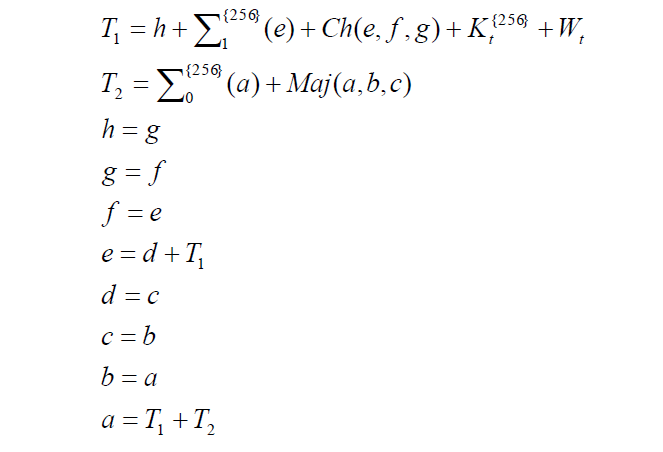
让我们来看看 T(1) 和 T(2) 的计算。
两个求和运算过程如下
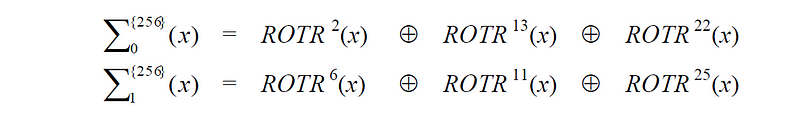
同样,Ch(e,f,g) 和 Maj(a,b,c) 的运算过程如下

Ch(e,f,g) 操作
运算结果 Ch(e,f,g) 分别根据 e 中对应的位是 1 还是 0,从 f 和 g 中选择每个位。
Maj(a,b,c) 操作
对于 Maj(a,b,c),该函数输出 a、b 和 c 中每个比特位置的多数值。
步骤 10:更新初始 H 值
将初始 H(0)(n)值添加到变量 a 至 h 中,即可重新计算出 H(0)(n)值。

步骤 11:连接最终的 H 值
最后,将所有更新的 H 值(H(f)(n))连接起来,就得到了输入字符串的最终 SHA-256 哈希值。
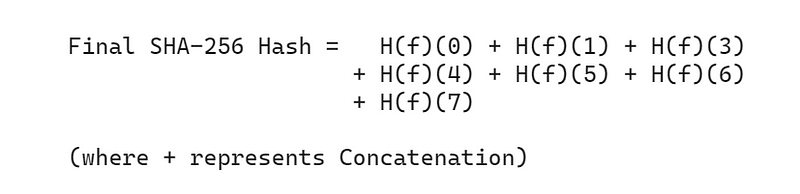
这就是我们生成 SHA-256 哈希值的整个过程。
这种算法在数学上是密集的、重复的、枯燥的,我明白为什么要这样做。
为什么不可逆转?
这是因为巧妙地使用了位逻辑运算(移位、旋转、Maj 等),而这些运算并没有直接的逆运算。
将它们应用于我们的多轮输入,会使输入不可逆转地乱码化。
此外,通过对素数的多次运算得出常量(H 值和 K 值),并根据输入比特使用这些常量,也为算法增加了所需的随机性,这使得算法的逆向工程过程显然是不可能的。



评论区